Menu
Optimisation du retour à l’équilibre d’un pendule contrôlé
Projet académique approfondi · CY Tech · 2025
Avec l’accompagnement scientifique de Badre Mounda (chercheur en géométrie algébrique)
Objectif : Ramener un pendule simple à l’équilibre en temps fini, tout en minimisant un coût quadratique sur la commande h(t), dans un cadre de contrôle optimal linéaire-quadratique.
- Schéma d’Euler explicite pour la simulation numérique du mouvement.
- Discrétisation du problème d’optimisation sous contraintes affines.
- Mise en œuvre d’un algorithme de gradient projeté.
- Formulation variationnelle, existence et unicité (théorème de Lax–Milgram).
- Obtention d’une équation d’Euler–Lagrange d’ordre 4.
- Vérification par une approche hamiltonienne (principe de Pontryagin).
Schéma du pendule : forces et angle θ
Le système est un pendule simple, la tige étant considérée inextensible et sans masse. L’application du principe fondamental de la dynamique à la masselotte conduit à une équation différentielle de d'ordre 2 qui relie l’angle θ(t) et son accélération.
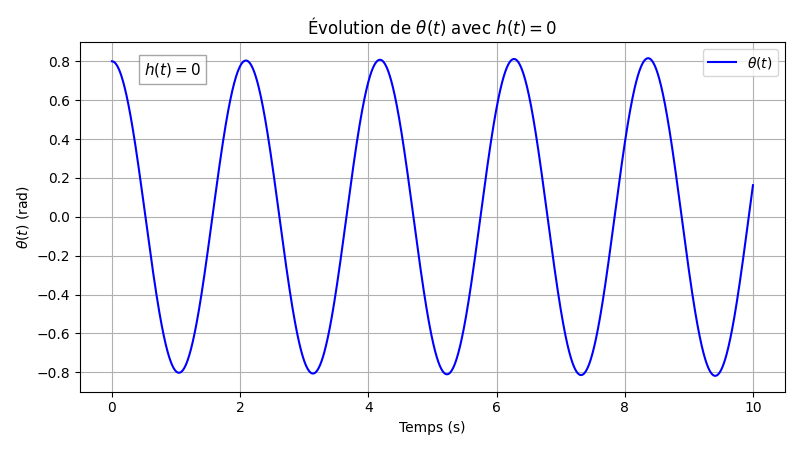
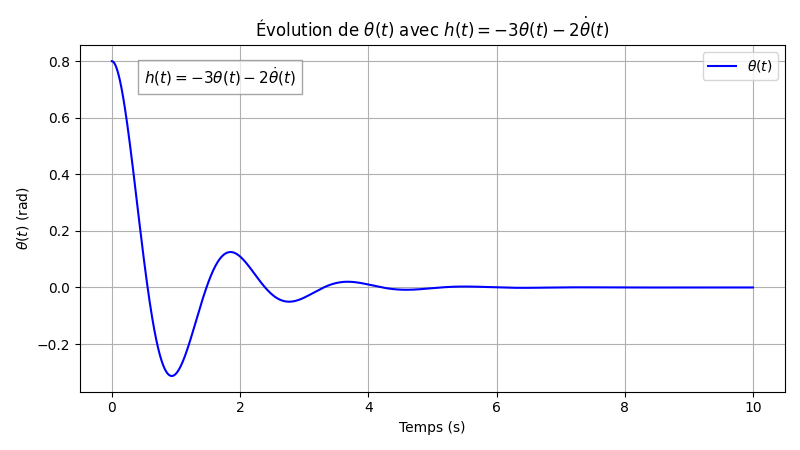
Dans un cadre idéal sans frottement, le pendule conserve son énergie : il oscille périodiquement et ne revient jamais naturellement à l’équilibre stable. On constate qu’il est possible de définir une commande qui amortit les oscillations du pendule.
Après avoir vérifié empiriquement la faisabilité d’une stabilisation, le projet pose la question suivante : quelle commande minimise l’énergie dépensée tout en assurant un retour rapide ? C’est le cœur du problème d’optimisation traité dans le rapport.
Si l’aperçu ne s’affiche pas correctement, utilisez “Ouvrir le PDF”.