Menu
Optimization of the return to equilibrium of a controlled pendulum
Advanced academic project · CY Tech · 2025
With scientific mentoring from Badre Mounda (researcher in algebraic geometry)
Objective: Bring a simple pendulum back to equilibrium in finite time while minimising a quadratic cost on the control h(t), within a linear–quadratic optimal control framework.
- Explicit Euler scheme for the numerical simulation of the dynamics.
- Discretisation of the optimisation problem under affine constraints.
- Implementation of a projected gradient algorithm.
- Variational formulation; existence and uniqueness (Lax–Milgram theorem).
- Derivation of a fourth-order Euler–Lagrange equation.
- Verification via a Hamiltonian approach (Pontryagin’s principle).
Pendulum diagram: forces and angle θ
The system is a simple pendulum, the rod being considered inextensible and massless. Applying Newton’s second law to the bob leads to a second-order differential equation relating the angle θ(t) to its acceleration.
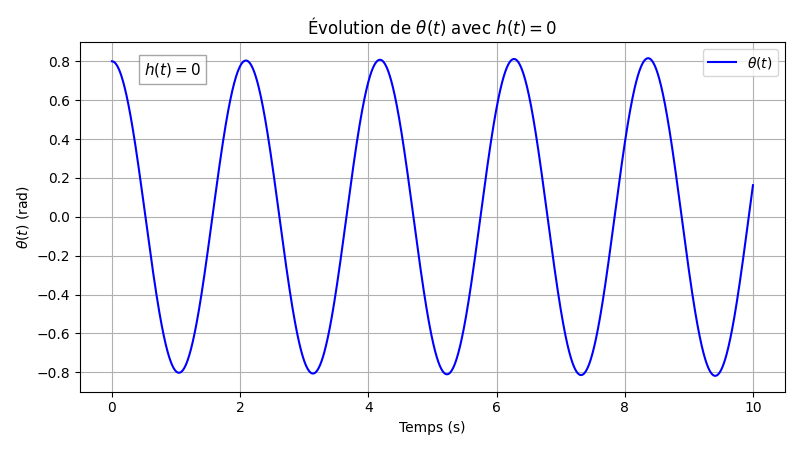
In an ideal frictionless setting, the pendulum conserves its energy: it oscillates periodically and never naturally returns to the stable equilibrium. It can be shown that a control input can be defined to damp the oscillations of the pendulum.
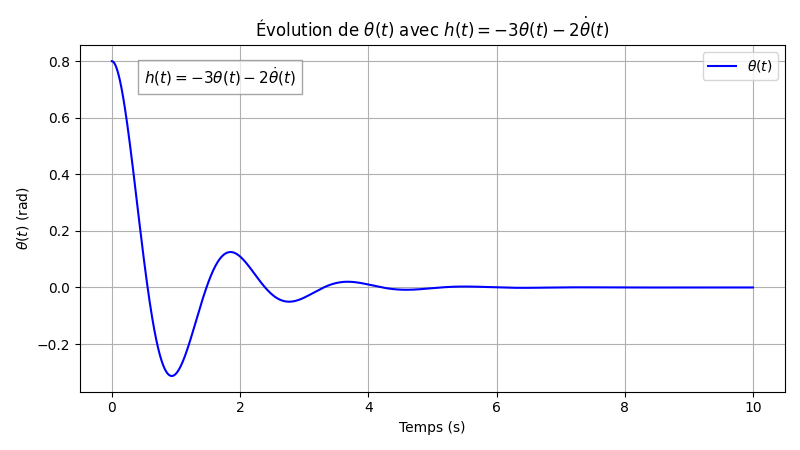
After empirically verifying the feasibility of stabilization, the project addresses the following question: which control minimizes the energy expenditure while ensuring a fast return? This is the core of the optimization problem studied in the report.
If the preview does not display correctly, please use “Open PDF”.